[2008-04-18] MC Escher lizard vector art

Escher's lizard is probably the best known complex tesselation. I saw a house once somewhere in Austin with a front walk made out of Escher-lizard paving stones. I've tried valiantly to find these stones many times since; they were Boing-Boinged once some time ago but the links there have since gone dead, I imagine due to licensing problems with the Escher estate. I myself have many clever schemes for projects involving Escher-lizard tiles, but I've been surprised to find that no decent vector art appears to be available in the public domain. There are some raster images here and there, but most of these are not geometrically perfect, as they must be to properly tile the plane ad infinitum. Even Escher's original art deviates significantly from geometric perfection, and raster images are in any case very inconvenient to work with for tiling applications.
Accordingly, I have taken it upon myself to produce the necessary vector art and make it available, here, in the public domain. I have posted W3C .SVG, Adobe Illustrator CS2 .AI, and AutoCad .DWG versions. I would emphasize to any who are concerned that this is not any type of photographic or photostatic reproduction; this is a redrawing which I produced myself using Adobe Illustrator, which is a convenient tool for performing the precise construction of the lizard's form using rotational transforms. This was an interesting process in itself, because it exposes one of the many processes whereby original tesselations can be constructed. This is a very complicated mathematics, and I can't even begin to treat it systematically. Those who are interested in learning more practical tricks for making tesselations are referred to Jinny Beyer's beautiful book Designing Tessellations : The Secrets of Interlocking Patterns.
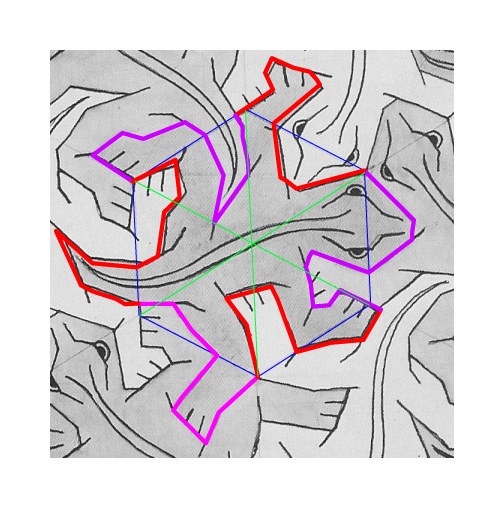
The above image illustrates the redrawing process. The underlying grayscale graphic is Escher's original. The three green lines were drawn first; these connect the opposing vertices of Escher's original hexagonal cell, and of necessity intersect in its center. Note even at this small scale a visible eccentricity in their intersection--Escher's hexagon is slightly imperfect, which is unsurprising given that it was constructed by hand. The blue hexagon is my cell, generated by computer and centered to the best of my ability on the intersection of the three green lines, and rotated with its vertices at their endpoints. The pink sections of the lizard's profile were manually traced over the original art using Illustrator's line tool. The red sections of the profile are merely rotations of the pink sections by 120 degrees about one adjacent vertex of the hexagon. Finally, the internal details of the lizard were added using various line, pen, and shape tools.
It is in the red, rotated sections where the deviations of Escher's original from the geometric ideal are apparent. Certainly my hand and eye are not a perfect tracing machine, and certainly there may be some small error in my location of Escher's original cell, but even without my superpositions, careful study of the original will reveal small descrepancies between one profile and its rotation. I think anyone who accepts my invitation to try the experiment for themselves will come to agree that there are, in fact, small flaws in the original. These are "flaws," of course, only in the abstract, geometric, platonic sense; aesthetically they are anything but. Indeed, these subtle variations are what identifies the original as the work of a human being, and not a machine, and hence make it art instead of just a mathematical exercise.
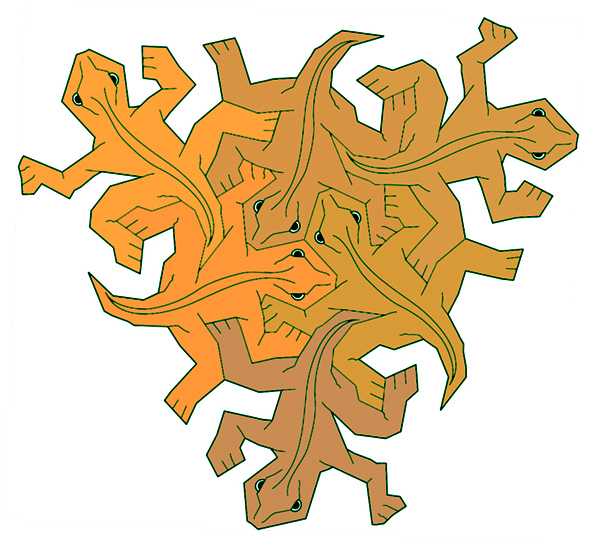
Finally, a note about coloration of tilings. Escher's lizards are commonly depicted in a three-color tiling, which of course is the minimum number of colors required to ensure that no two edges of like-colored tiles ever meet. This scheme is prone to garishness; if one has to use three-color tiling, it's always best to adhere to Edward Tufte's principle of least perceptible difference and choose shades that are only very slightly different from one another. Otherwise, the spatial rhythym of the colors sets up a kind of dizzying moire effect in the tiled plane. My own preference is for subtle, natural, random color variations between tiles. I dream of Escher lizards executed in Saltillo.
last modified 2008-04-18